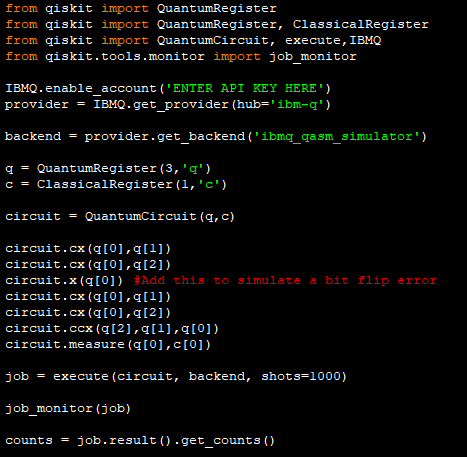
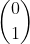print('\n Quantum Full Adder')
print('---------------------')
from qiskit import QuantumRegister
from qiskit import ClassicalRegister
from qiskit import QuantumCircuit, execute,IBMQ
from qiskit.tools.monitor import job_monitor
IBMQ.enable_account('INSERT API TOKEN HERE')
provider = IBMQ.get_provider(hub='ibm-q')
######## A ###########################
q = QuantumRegister(5,'q')
c = ClassicalRegister(2,'c')
circuit = QuantumCircuit(q,c)
circuit.x(q[0])
circuit.cx(q[0],q[3])
circuit.cx(q[1],q[3])
circuit.cx(q[2],q[3])
circuit.ccx(q[0],q[1],q[4])
circuit.ccx(q[0],q[2],q[4])
circuit.ccx(q[1],q[2],q[4])
circuit.measure(q[3],c[0])
circuit.measure(q[4],c[1])
########################################
backend = provider.get_backend('ibmq_qasm_simulator')
job = execute(circuit, backend, shots=1)
print('\nExecuting...\n')
print('\nA\n')
job_monitor(job)
counts = job.result().get_counts()
print('RESULT: ',counts,'\n')
######## B ###########################
q = QuantumRegister(5,'q')
c = ClassicalRegister(2,'c')
circuit = QuantumCircuit(q,c)
circuit.x(q[1])
circuit.cx(q[0],q[3])
circuit.cx(q[1],q[3])
circuit.cx(q[2],q[3])
circuit.ccx(q[0],q[1],q[4])
circuit.ccx(q[0],q[2],q[4])
circuit.ccx(q[1],q[2],q[4])
circuit.measure(q[3],c[0])
circuit.measure(q[4],c[1])
######################################
job = execute(circuit, backend, shots=1)
print('\nB\n')
job_monitor(job)
counts = job.result().get_counts()
print('RESULT: ',counts,'\n')
######## A + B ###########################
q = QuantumRegister(5,'q')
c = ClassicalRegister(2,'c')
circuit = QuantumCircuit(q,c)
circuit.x(q[0])
circuit.x(q[1])
circuit.cx(q[0],q[3])
circuit.cx(q[1],q[3])
circuit.cx(q[2],q[3])
circuit.ccx(q[0],q[1],q[4])
circuit.ccx(q[0],q[2],q[4])
circuit.ccx(q[1],q[2],q[4])
circuit.measure(q[3],c[0])
circuit.measure(q[4],c[1])
######################################
job = execute(circuit, backend, shots=1)
print('\nA + B\n')
job_monitor(job)
counts = job.result().get_counts()
print('RESULT: ',counts,'\n')
######## Cin ###########################
q = QuantumRegister(5,'q')
c = ClassicalRegister(2,'c')
circuit = QuantumCircuit(q,c)
circuit.x(q[2])
circuit.cx(q[0],q[3])
circuit.cx(q[1],q[3])
circuit.cx(q[2],q[3])
circuit.ccx(q[0],q[1],q[4])
circuit.ccx(q[0],q[2],q[4])
circuit.ccx(q[1],q[2],q[4])
circuit.measure(q[3],c[0])
circuit.measure(q[4],c[1])
######################################
job = execute(circuit, backend, shots=1)
print('\nCin\n')
job_monitor(job)
counts = job.result().get_counts()
print('RESULT: ',counts,'\n')
######## Cin + A ###########################
q = QuantumRegister(5,'q')
c = ClassicalRegister(2,'c')
circuit = QuantumCircuit(q,c)
circuit.x(q[2])
circuit.x(q[0])
circuit.cx(q[0],q[3])
circuit.cx(q[1],q[3])
circuit.cx(q[2],q[3])
circuit.ccx(q[0],q[1],q[4])
circuit.ccx(q[0],q[2],q[4])
circuit.ccx(q[1],q[2],q[4])
circuit.measure(q[3],c[0])
circuit.measure(q[4],c[1])
######################################
job = execute(circuit, backend, shots=1)
print('\nCin + A\n')
job_monitor(job)
counts = job.result().get_counts()
print('RESULT: ',counts,'\n')
######## Cin + B ###########################
q = QuantumRegister(5,'q')
c = ClassicalRegister(2,'c')
circuit = QuantumCircuit(q,c)
circuit.x(q[2])
circuit.x(q[1])
circuit.cx(q[0],q[3])
circuit.cx(q[1],q[3])
circuit.cx(q[2],q[3])
circuit.ccx(q[0],q[1],q[4])
circuit.ccx(q[0],q[2],q[4])
circuit.ccx(q[1],q[2],q[4])
circuit.measure(q[3],c[0])
circuit.measure(q[4],c[1])
######################################
job = execute(circuit, backend, shots=1)
print('\nCin + B\n')
job_monitor(job)
counts = job.result().get_counts()
print('RESULT: ',counts,'\n')
######## Cin + A + B ###########################
q = QuantumRegister(5,'q')
c = ClassicalRegister(2,'c')
circuit = QuantumCircuit(q,c)
circuit.x(q[2])
circuit.x(q[1])
circuit.x(q[0])
circuit.cx(q[0],q[3])
circuit.cx(q[1],q[3])
circuit.cx(q[2],q[3])
circuit.ccx(q[0],q[1],q[4])
circuit.ccx(q[0],q[2],q[4])
circuit.ccx(q[1],q[2],q[4])
circuit.measure(q[3],c[0])
circuit.measure(q[4],c[1])
######################################
job = execute(circuit, backend, shots=1)
print('\nCin + A + B\n')
job_monitor(job)
counts = job.result().get_counts()
print('RESULT: ',counts,'\n')
print('Press any key to close')
input()